Ажурная модель
Существует несколько типов оригами-додекаэдров, но сделать эту прозрачную конструкцию из бумажных модулей проще всего. Хорошее задание для детей, желающих познакомиться с азами пространственной геометрии и взрослых, ищущих эффективное средство для снятия стресса. Желательно использовать для игрушки бумагу ками с рисунком, она придаст особый шарм и колорит.
Пошаговая инструкция:
- Для создания кусудамы понадобится 30 одинаковых модулей. Их складывают из прямоугольников, имеющих соотношение сторон 3:4. Например, размером 6х8 см, 9х12 см и так далее. Можно брать как одно-, так и двухсторонние листы.
- Складываем каждый прямоугольник пополам вдоль длинной стороны. После чего делаем Z-образный сгиб.
- Располагаем получившуюся полоску длинной стороной к себе. Загибаем правый нижний угол вверх. Переворачиваем заготовку на 180°. И повторяем действие для правого нижнего угла (другого).
- Складываем фигуру по диагонали, как показано на рис 4.
- Модули для додекаэдра-кусудамы готовы.
Остаётся соединить их в пространственную композицию. Для этого короткую часть одного модуля вставляем к «карман» длинной части другого. И располагаем так, чтобы внутренние углы и грани обоих элементов совпали.
Аналогичный образом добавляем третий модуль, соединяя его с предыдущими двумя и формируя устойчивый конструктивный узел.
Продолжаем крепить детали друг к другу, пока не получится объёмная фигура.
За счёт необычной бумаги с принтом, получается стильный предмет декора. Чтобы кусудама не распадалась, лучше соединить узловые элементы с помощью клея.
Подробная сборка ажурного додекаэдра представлена и в видео-МК:
Собираем простые фигурки из бумаги своими руками: стаканчик
Очень легко и просто можно сделать из бумажной материи стаканчик, который можно использовать по различным назначениям. Такой вариант бумажной поделки будет легко выполнимым даже для детей разных возрастов.
Вам необходимо взять лист бумаги белого цвета или любого другого цветового оттенка.
Размеры бумажной основы должны быть А4. Подготовленный лист сложите по диагональному направлению, и отрежьте все излишки. У вас должен сформироваться квадрат, который вам необходимо сложить по диагональному направлению для оформления фигуры треугольника.
Теперь необходимо концы треугольника. Расположенные в верхней части конструкции загнуть в разные стороны и разогнуть обратно. Далее правый нижний уголок треугольника загните по направлению влево до точки предыдущего загибания верхней части фигуры. Теперь нижний уголок с левого края загните по направлению вправо. Теперь вам следует разделить верхние уголки треугольника. Уголок, который располагается спереди, заложите в кармашек, а задний загните назад.
Теперь вам следует сжать боковые стороны бумажного стаканчика таким образом, чтобы у вас разделились все верхние слои вашей конструкции оригами. Теперь ваш стаканчик из бумаги готов.
Кусудама из правильных пятиугольников
Схема сборки додекаэдра-оригами из пентагонов – равносторонних пятиугольников, разработана американским дизайнером Дэвидом Брилом. Для модулей он использует 12 листов формата А6, то есть 10,5х14,8 см.
Пошаговая инструкция:
- Исходный прямоугольник складываем пополам в продольном и поперечном направлении, намечая серединные оси.
- Правый верхний и левый нижний угол сгибаем к центру. Получаем своего рода полуконверт.
- Аналогично складываем противоположные углы.
- Пятиугольную заготовку, «закрываем» сверху вниз «долиной».
- Верхний угол опускаем вниз и возвращаем обратно. На месте пересечения получившейся линии с вертикальной осью фигуры, образуется точка. К ней поочерёдно сгибаем внешние углы.
- Модуль-пентагон готов. Последние два сгиба раскрываем – это будут детали крепления элементов между собой.
- Боковые «ушки» одной детали вставляем в «карманы» другой. Места соединения для надёжности фиксируем клеем.
- Продолжаем сборку, пока не используем все 12 модулей.
Из подобных додекаэдров часто делают настольные календари. На каждой грани как раз размещается по месяцу. Соответствующие распечатки с числами и днями недели, можно скачать из интернета и наклеить на стенки модели. Получится не только красиво, но и практично.
Интересные факты о додекаэдре
Правильные многогранники с древних времен восхищали человечество и служили прообразом мирового устройства. Как оказалось, подобные представления небезосновательны. В 2003 году, анализируя данные исследовательского аппарата WMAP, запущенного NASA для изучения фоновых космических излучений, учёные выдвинули гипотезу о додекаэдрическом строении Вселенной по принципу сферы Пуанкаре.
Нечто подобное предполагал и живший в V в. до н. э. древнегреческий философ Платон. В своём учении о классических стихиях, он назвал додекаэдр «образцом божественного устройства Космоса». Вообще же все пять известных правильных многогранников до сих пор называют Платоновыми телами, по имени мыслителя, впервые выстроившего с их помощью чёткую картину мироздания.
Пентагон, лежащий в основе додекаэдра, построен на принципах «золотого сечения». Эта пропорция, которую древние греки считали «божественной» часто встречается в природе. Интересно, что соотношения «золотого сечения» присущи лишь додекаэдру и икосаэдру, у трёх других Платоновых тел его нет.
Игрушки древних римлян
На территориях Европы, некогда принадлежавших Римской империи, до сих пор находят загадочные бронзовые фигурки в форме додекаэдра. Предметы пустотелые, с круглыми отверстиями на каждой стороне и шариками, обозначающими вершины. Учёные пока не смогли однозначно определить функцию этих объектов. Первоначально считалось, что это своеобразные игрушки, однако позднее их отнесли к предметам культа, символизирующим устройство Вселенной. Или Земли, согласно теории, последовательно выдвигаемой с XIX века мировыми физиками, в том числе и российскими.
Впервые о том, что наша планета представляет собой кристалл додекаэдрической формы, заговорили французский математик Пуанкаре и геолог-исследователь де Бемон. Они утверждали, что земная кора, словно футбольный мяч, состоит из 12 правильных пятиугольников, в местах соединения которых, располагаются аномальные зоны и планетарные силовые поля.
В 1920-х годах идею французских коллег подхватил русский физик Степан Кислицын. Он пошёл ещё дальше, заявив, что планета не остаётся в стабильном состоянии, она растёт, из додекаэдра постепенно трансформируясь в икосаэдр. Учёный разработал модели подобных изменений, обозначив узлы гигантской кристаллической сетки, где, по его мнению, располагались месторождения полезных ископаемых: угля, нефти, газа и так далее. В 1928 году Кислицын, опираясь на свои исследования, указал на поверхности земного шара 12 алмазоносных центров, из которых 7 к настоящему времени находятся в активной разработке.
Идеи кристаллического строения планеты продолжают развиваться в XXI веке. Согласно последней гипотезе, подобная структура свойственна всем живым организмам, не только космическим телам, но и человеку. Тем интереснее будет собирать додекаэдр-оригами, чувствуя свою сопричастность к великим тайнам Вселенной.
Додекаэдр-звезда
Правильные звёздчатые многогранники относятся к самым красивым геометрическим фигурам. С момента своего открытия в XVI веке, они считались символом совершенства Вселенной. Малый звёздчатый додекаэдр впервые построил немецкий астроном и математик Иоганн Кеплер – создатель знаменитой теории о строении Солнечной системы. Многогранник имеет собственное имя: Арур Кэли, в честь английского учёного, сделавшего огромный вклад в развитие линейной алгебры.
Малый звёздчатый додекаэдр-оригами представляет собой фигуру из 12 граней-пентаграмм, с пятью пентаграммами, сходящимися к вершинам. Он состоит из 30 модулей, которые складываются из квадратов, размером 8х8 см. Лучше всего использовать профессиональную бумагу-оригами, которая позволит создавать чёткие грани и жёсткие узлы, не позволяющие конструкции распадаться или деформироваться.
Правильные многогранники с древних времен восхищали человечество и служили прообразом мирового устройства. Как оказалось, подобные представления небезосновательны. В 2003 году, анализируя данные исследовательского аппарата WMAP, запущенного NASA для изучения фоновых космических излучений, учёные выдвинули гипотезу о додекаэдрическом строении Вселенной по принципу сферы Пуанкаре.
Нечто подобное предполагал и живший в V в. до н. э. древнегреческий философ Платон. В своём учении о классических стихиях, он назвал додекаэдр «образцом божественного устройства Космоса». Вообще же все пять известных правильных многогранников до сих пор называют Платоновыми телами, по имени мыслителя, впервые выстроившего с их помощью чёткую картину мироздания.
Пентагон, лежащий в основе додекаэдра, построен на принципах «золотого сечения». Эта пропорция, которую древние греки считали «божественной» часто встречается в природе. Интересно, что соотношения «золотого сечения» присущи лишь додекаэдру и икосаэдру, у трёх других Платоновых тел его нет.
Игрушки древних римлян
На территориях Европы, некогда принадлежавших Римской империи, до сих пор находят загадочные бронзовые фигурки в форме додекаэдра. Предметы пустотелые, с круглыми отверстиями на каждой стороне и шариками, обозначающими вершины. Учёные пока не смогли однозначно определить функцию этих объектов. Первоначально считалось, что это своеобразные игрушки, однако позднее их отнесли к предметам культа, символизирующим устройство Вселенной. Или Земли, согласно теории, последовательно выдвигаемой с XIX века мировыми физиками, в том числе и российскими.
Впервые о том, что наша планета представляет собой кристалл додекаэдрической формы, заговорили французский математик Пуанкаре и геолог-исследователь де Бемон. Они утверждали, что земная кора, словно футбольный мяч, состоит из 12 правильных пятиугольников, в местах соединения которых, располагаются аномальные зоны и планетарные силовые поля.
В 1920-х годах идею французских коллег подхватил русский физик Степан Кислицын. Он пошёл ещё дальше, заявив, что планета не остаётся в стабильном состоянии, она растёт, из додекаэдра постепенно трансформируясь в икосаэдр. Учёный разработал модели подобных изменений, обозначив узлы гигантской кристаллической сетки, где, по его мнению, располагались месторождения полезных ископаемых: угля, нефти, газа и так далее. В 1928 году Кислицын, опираясь на свои исследования, указал на поверхности земного шара 12 алмазоносных центров, из которых 7 к настоящему времени находятся в активной разработке.
Идеи кристаллического строения планеты продолжают развиваться в XXI веке. Согласно последней гипотезе, подобная структура свойственна всем живым организмам, не только космическим телам, но и человеку. Тем интереснее будет собирать додекаэдр-оригами, чувствуя свою сопричастность к великим тайнам Вселенной.
Большой выбор развёрток простых геометрических фигур.
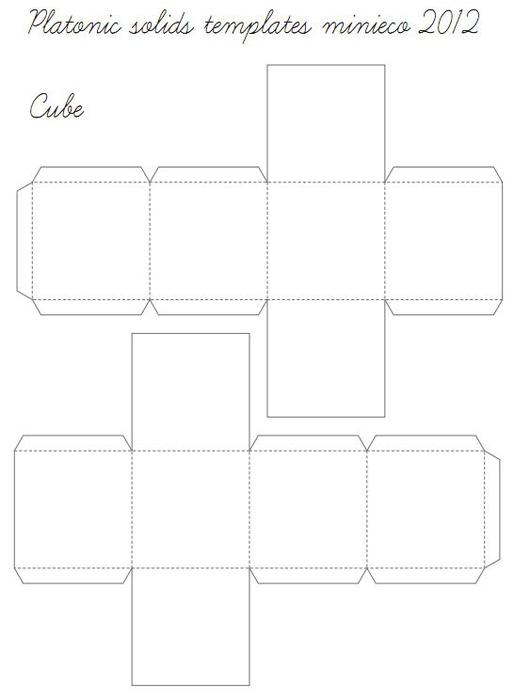
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы , а также читайте, как распечатывать из автокада . Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров:)
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура — конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура — ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
Создавать поделки своими руками интересно не только детям, но и взрослым. Однако для взрослых придумано достаточное количество моделей, которые отличаются сложностью выполнения и временем, затраченным на их создание. В последнее время у взрослых и детей появился интерес к созданию сложных геометрических фигур. К такому виду фигур относится икосаэдр, который представляет собой правильный многоугольник и является одним из платоновых тел – правильных многогранников. Эта фигура имеет 20 треугольных граней (равносторонних треугольников), 30 ребер и 12 вершин, которые являются местом стыка 5 ребер. Правильный икосаэдр из бумаги собрать достаточно сложно, но интересно. Если вы увлечены оригами, то сделать икосаэдр бумажный своими руками вам не составит труда. Его сделать из цветной, гофрированной бумаги, фольги, упаковочной бумаги для цветов. Используя разнообразные материалы, можно придать еще большую красоту и эффектность своему икосаэдру. Все зависит только от фантазии его создателя и подручного материала, имеющегося на столе.
Предлагаем вам несколько вариантов разверток икосаэдра, которые можно распечатать, перенести на плотную бумагу и картон, согнуть по линиям и склеить.
Как сделать икосаэдр из бумаги: схема
Для того чтобы собрать икосаэдр из листа бумаги или картона, необходимо предварительно подготовить следующие материалы:
- макет икосаэдра;
- клей ПВА;
- ножницы;
- линейка.
Во время создания икосаэдра важно обратить особое внимание на процесс сгиба всех деталей: для того, чтобы ровно согнуть бумагу, можно использовать обычную линейку.
Примечательно, что икосаэдр можно встретить и в повседневной жизни. Например, в форме усеченного икосаэдра (многогранник, состоящий из 12 пятиугольников и 20 шестиугольников правильной формы) выполнен футбольный мяч. Это особенно видно, если раскрасить получившийся икосаэдр в черно-белый цвет, как и сам мяч.
Такой футбольный мяч можно сделать самостоятельно, распечатав предварительно развертку усеченного икосаэдра в 2 экземплярах:
Создание икосаэдра своими руками представляет интересный процесс, который требует вдумчивости, терпения и большого количества бумаги. Однако результат, полученный в итоге, будет радовать глаз еще долгое время. Икосаэдр можно дать поиграть ребенку, если он достиг уже трехлетнего возраста. Играя с такой сложной геометрической фигурой, он будет развивать не только образное мышление, пространственные навыки, но и знакомиться с миром геометрии. Если же взрослый решил создать икосаэдр самостоятельно, то такой творческий процесс по конструированию икосаэдра позволит скоротать время, а также похвастаться перед близкими своим умением создавать сложные фигуры. Поделки с детьми. ФУТБОЛЬНЫЙ МЯЧ И МНОГОГРАННИКИ ИЗ ЦВЕТНОЙ БУМАГИ. Среди моих читателей очень много воспитателей Детских садиков и руководителей Художественных кружков, в связи с этим, я изредка публикую посты с поделками вместе с детьми и для детей.
Кстати, всем родителям хочу порекомендовать очень хорошую детскую студию «Теремок», которая существует уже два года и зарекомендовала себя одной из самых лучших студий в воспитательно-образовательной работе с детьми. «Теремок» поможет вашему малышу находить общий язык в общении со сверстниками, разовьет уважение к старшим, развлечет, устраивая праздники и конкурсы и многое-многое другое. Очень нужно, детям, с самого раннего возраста, прививать любовь к творчеству. Это вырабатывает у них любознательность, расширяет кругозор, прививает любовь к труду. В студии есть очень хороший художественный кружок по разным видам и жанрам изобразительного искусства. Подробнее о студии вы сможете узнать на сайте — https://teremok64.ru.
А сейчас, предлагаю вам занять детей и сделать вместе с ними многогранники из цветной бумаги. Это не только увлечет их, они получат первые знания в математике. Ниже, под катом, пять шаблонов на некоторые многоугольники, которые нужно распечатать и увеличить. Все очень легко и просто, вырезать, согнуть и склеить. Очень красивая гирлянда, яркая, веселая и солнечная)
Можете сделать макет футбольного мяча. Для этого, желательно, взять бумагу — поплотнее.
Во вложении, шаблон мяча в натуральную величину, состоит из восьми страниц.
Вложение:
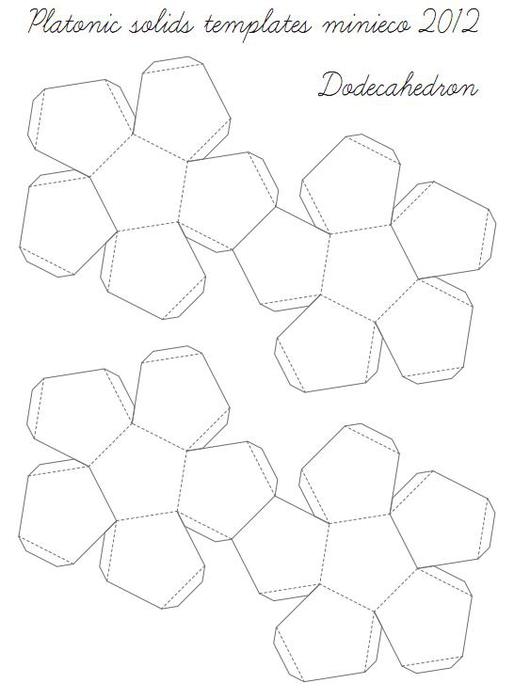
ДОДЕКАЭДР
ИКОСАЭДР
ОКТАЭДР
ТЕТРАЭДР
Вырезать шаблоны и согнуть по пунктирным линиям
ВУАЛЯ. Можете их собрать на ниточку и сделать математическую гирлянду)
Много интересного можно найти для себя в тех сферах науки, которые, казалось бы, никогда не пригодятся в привычной жизни простого обывателя. Например, геометрия, о которой большинство забывают, только лишь переступив порог школы. Но странным образом малознакомые области науки становятся очень увлекательными, если с ними столкнуться поближе. Вот и геометрическая развертка многогранника — совершенно ненужная в повседневной жизни вещь — может стать началом увлекательного творчества, способного захватить и детей, и взрослых.
Об изготовление своими руками моделей многогранников из бумаги
| Главная | Многогранники | Звезды | Галерея | Экспорт | Из бумаги | Лаборатория | Гостевая |
Даже беглый взгляд на галерею многогранников доказывает, что звёздчатые многогранники являются очень красивыми и декоративными. Совсем не сложно своими руками изготовить модель понравившегося многогранника из бумаги или картона. Всё, что требуется для создания бумажной модели — цветной картон, ножницы и клей.
Наиболее фундаментальным русскоязычным руководством по изготовлению бумажных моделей многогранников является книга: Веннинджер «Модели многогранников», 1974
Смотреть список моделей
, , книга-онлайн.
В ней даются подробные инструкции по изготовлению 119-ти бумажных моделей многогранников, в том числе всех 75 однородных многогранников (включая правильные и полуправильные выпуклые и звездчатые многогранники), а также наиболее красивых звездчатых форм икосаэдра, икосододекаэдра и кубооктаэдра. В книге приводятся трафареты и шаблоны для вырезания из бумаги составных частей будущей модели (заготовок), а также даются схемы соединения частей между собой и таблицы раскраски. В тоже время читателю оставлена свобода для творчества: для некоторых моделей Веннинджер предлагает самостоятельно найти способ соединения деталей, дающий требуемую раскраску, или подумать над возможными вариантами раскраски. После прочтения книги Веннинджера вы научитесь самостоятельно проектировать новые звездчатые формы и изготавливать их модели из бумаги.
Изложение материала в книге Веннинджера эволюционное: в начале рассматривается понятие многогранника, описываются простые для понимания и изготовления модели правильных и полуправильных выпуклых многогранников (см. таблицу). Затем вводится понятие звездчатых форм, трехмерный калейдоскоп, анализируются принципы построения звездоформ и рассматриваются соответствующие бумажные модели. Завершается книга математическим определением и изготовлением моделей всех невыпуклых однородных многогранников, в том числе очень сложных «курносых» моделей. По причине эволюционности желательно читать книгу с самого начала, по крайней мере следует прочитать общие указания об изготовлении моделей, замечания о звездчатых формах и соединениях, а при изготовлении более сложных моделей надо читать соответствующие предварительные замечания. Единственный недостаток книги — увы, не цветные фотографии готовых моделей. Впрочем, вы можете смотреть интерактивные трехмерные модели соответствующих многогранников на этом сайте: в следующей таблице перечислены все модели из книги Веннинджер и даны ссылки на трехмерные модели и инструкции Веннинджера по изготовлению моделей многогранников из бумаги (чтобы увидеть примерный внешний вид готовой модели из бумаги, подведите курсор к соответствующей ссылке).
В нашей стране весомый вклад в изготовление и популяризацию бумажных моделей многогранников внесла Гончар Валентина Васильевна, архитектор и руководитель кружка бумажного моделирования. Её книги «Кристаллы» (1994) и «Модели многогранников» (1997, 2010) посвящены в основном платоновым и архимедовым телам, а также их отдельным звездчатым формам. Гончар В.В. предлагает упростить создание бумажных моделей за счет использования не заготовок отдельных граней, а единой выкройки, что сделает моделирование доступным даже для детей. Значительно преуспели в создании единых трафаретов и зарубежные авторы, причем трафареты найдены не только для выпуклых многогранников, но и даже для некоторых невыпуклых многогранников. В таблице ниже для примера даны ссылки на соответствующие трафареты и фотографии бумажных моделей сайта www.polyhedra.net. Впрочем, математику соответствующее упрощение раскраски моделей (вплоть до одноцветной) может показаться некоторым недостатком.
Другое направление, развитое Валентиной Васильевной — создание моделей многогранников в технике оригами (в идеале, без использования клея и ножниц). Ею создан «универсальный модуль оригами», складывая который можно получать отдельные звездчатые многогранники, и даже делать оригинальные подвижные модели — трансформеры. Созданная Валентиной модель-трансформер «раскрывающийся цветок» (видео, инструкции по изготовлению) получила всемирное признание.

, т.е. создание красивых цветных шаров из бумаги. Некоторые кусудамы сами являются многогранниками, другие лишь сохраняют хорошо заметную симметрию правильных многогранников. Основная цель кусудам — эстетичный внешний вид бумажных моделей, кусудамы часто украшают бусинками, кисточками и т.д., о математической стрости в раскраске и строении речь не идет (впрочем, несомненна связь групп симметрии многогранников и внешней привлекательности кусудам). Приведенные примеры фотографий кусудами взяты с сайта https://ru-kusudama.livejournal.com.
В 2011 году издательство «Многогранники» поставило изготовление многогранников из бумаги на надежные коммерческие рельсы. Оно выпускает наборы «Волшебные грани». Каждый набор посвящен конкретному многограннику и содержит вырезанные и подогнанные детали, а также инструкции по изготовлению. Следует отметить отлично оформленный сайт, содержащий фотографии готовых моделей, видеоинструкции по их изготовлению (конечно, только из соответствующих наборов) и другие материалы. К сожалению, пока номенклатура многогранников из наборов «Волшебные грани» весьма ограничена; в таблице ниже представлен список ссылок на многогранники, для которых издавались наборы «Волшебные грани».
О сложности изготовления бумажных моделей многогранников
В столбце «Сложность» таблицы указано число деталей (граней), из которых состоит многогранник, а также количество различных типов шаблонов, которые потребуются для изготовления этих деталей из бумаги. Конечно, такое количество деталей потребуется, только если при изготовлении бумажной модели многогранника смежные грани раскрашиваются в различные цвета. Для однородных многогранников это оптимальный способ раскраски, но для звёздчатых форм и особенно соединений тел другая раскраска может оказаться более правильной и интересной. И всякий раз, когда смежные грани окрашиваются в одинаковый цвет, можно упростить изготовление модели, уменьшив количество заготовок и клеевых соединений. Например, модель «соединение пяти тетраэдров» имеет 60 граней (рисунок слева), но если каждый тетраэдр раскрашивать в свой цвет, то модель можно будет собрать всего из 20 деталей, по 4 детали каждого цвета (рисунок справа). В самом простом случае каждый выпуклый многогранник (а также некоторые не выпуклые) может быть изготовлен из единственной заготовки, однако при этом (если не использовать цветной принтер) получится лишь одноцветная модель. Впрочем, зачастую упрощенно раскрашенные или даже одноцветные бумажные модели многогранников весьма эффектны.
Таблица — многогранники, которые можно изготовить своими руками из бумаги
, даны ссылки на инструкции, схемы, развертки в различных источниках (чтобы увидеть примерный внешний вид готовой модели, подведите курсор к ссылке).
| Многогранник | Сложность (деталей / шаблонов) | Модель на zvzd3d.ru | Ссылки на инструкции, схемы, развертки многогранников из бумаги | ||
| 3d | gif | Веннинджер | Волшебные грани | polyhedra.net и другие | |
| Выпуклые правильные и полуправильные многогранники | |||||
| тетраэдр | 4/1 | 800000 | набор | есть, шаблон | |
| октаэдр | 8/1 | 800001 | набор | есть, шаблон | |
| куб | 6/1 | 800002 | набор | есть, шаблон | |
| икосаэдр | 20/1 | 800003 | набор | есть, шаблон | |
| додекаэдр | 12/1 | 800004 | набор | есть, шаблон | |
| усеченный тетраэдр | 8/2 | 800005 | набор | есть, шаблон | |
| усеченный октаэдр | 14/2 | 800006 | набор | есть, шаблон | |
| усеченный куб | 14/2 | 800007 | набор | есть, шаблон | |
| усеченный икосаэдр | 32/2 | 800008 | набор | есть, шаблон | |
| усеченный додекаэдр | 32/2 | 800009 | №10 | набор | есть, шаблон |
| кубооктаэдр | 14/2 | 800010 | №11 | набор | есть, шаблон |
| икосододекаэдр | 32/2 | 800011 | №12 | набор | есть, шаблон |
| ромбокубоктаэдр | 26/3 | 800012 | №13 | набор | есть, шаблон |
| ромбоикосододекаэдр | 62/3 | 800014 | №14 | набор | есть, шаблон |
| ромбоусеченный кубооктаэдр | 26/3 | 800015 | №15 | набор | есть, шаблон |
| ромбоусеченный икосододекаэдр | 62/3 | 800016 | №16 | набор | есть, шаблон |
| курносый куб | 38/3 | 800017 | №17 | набор | есть, шаблон |
| курносый додекаэдр | 92/3 | 800018 | №18 | набор | есть, шаблон |
| Звездчатые формы и соединения (создать новые) | |||||
| Звёздчатый октаэдр (stella octangula Кеплера) | 24/1 | 800201 | №19 | набор | есть, шаблон |
| малый звездчатый додекаэдр | 60/1 | 800019 | №20 | набор | есть, шаблон |
| большой додекаэдр | 60/1 | 800020 | №21 | набор | есть, шаблон |
| большой звездчатый додекаэдр | 60/1 | 800021 | №22 | набор | есть, шаблон |
| Соединение пяти октаэдров | 120/1 | 802003 | №23 | набор | есть, шаблон |
| Соединение пяти тетраэдров | 60/1 | 803803 | №24 | набор | есть, шаблон |
| Соединение десяти тетраэдров | 180/2 | 805603 | №25 | ||
| Первая звёздчатая форма икосаэдра | 60/1 | 802203 | №26 | набор |
от Светланы |
| Вторая звёздчатая форма икосаэдра | 300/3 | 800803 | №27 | ||
| Третья звёздчатая форма икосаэдра | 60/1 | 806603 | №28 |
от Светланы |
|
| Четвёртая звёздчатая форма икосаэдра | 180/2 | 807403 | №29 | ||
| Пятая звёздчатая форма икосаэдра | 300/3 | 806203* | №30 | набор | |
| Шестая звёздчатая форма икосаэдра | 120/2 | 806403 | №31 | набор | |
| Седьмая звёздчатая форма икосаэдра | 120/1 | 803203 | №32 | набор | есть, шаблон |
| Восьмая звёздчатая форма икосаэдра | 120/1 | 800603 | №33 | ||
| Девятая звёздчатая форма икосаэдра | 60/1 | 801403 | №34 | набор | |
| Десятая звёздчатая форма икосаэдра | 240/4 | 804403 | №35 | ||
| Одиннадцатая звёздчатая форма икосаэдра | 120/2 | 804203 | №36 | ||
| Двенадцатая звёздчатая форма икосаэдра | 180/2 | 803403 | №37 | ||
| Тринадцатая звёздчатая форма икосаэдра | 240/4 | 805403 | №38 | ||
| Четырнадцатая звёздчатая форма икосаэдра | 120/2 | 807003 | №39 | набор | |
| Пятнадцатая звёздчатая форма икосаэдра | 240/4 | 804603 | №40 | ||
| большой икосаэдр | 180/2 | 800022 | №41 | набор | есть, шаблон |
| Завершающая звёздчатая форма икосаэдра | 180/2 | 800203 | №42 | ||
| Соединение куба и октаэдра | 48/2 | 801210 | №43 | набор | есть, шаблон |
| Вторая звёздчатая форма кубооктаэдра | 96/2 | 801010 | №44 | ||
| Третья звёздчатая форма кубооктаэдра | 120/4 | 802410 | №45 | ||
| Завершающая звёздчатая форма кубооктаэдра | 72/3 | 800210 | №46 |
|
|
| Первая звёздчатая форма икосододекаэдра (соединение додекаэдра и икосаэдра) | 120/2 | 809611 | №47 | есть, шаблон | |
| Вторая звёздчатая форма икосододекаэдра | 240/2 | 809411 | №48 | ||
| Третья звёздчатая форма икосододекаэдра | 300/4 | 809011 | №49 | ||
| Четвёртая звёздчатая форма икосододекаэдра | 120/2 | 863611 | №50 | ||
| Пятая звёздчатая форма икосододекаэдра | 180/2 | 866411 | №51 | ||
| Шестая звёздчатая форма икосододекаэдра | 240/3 | 858011 | №52 | ||
| Седьмая звёздчатая форма икосододекаэдра | 240/2 | 882211 | №53 | ||
| Восьмая звёздчатая форма икосододекаэдра | 180/2 | 1057211 | №54 | ||
| Девятая звёздчатая форма икосододекаэдра | 420/4 | 1199611* | №55 | ||
| Десятая звёздчатая форма икосододекаэдра | 240/3 | 1305011* | №56 | набор | есть, шаблон |
| Одиннадцатая звёздчатая форма икосододекаэдра | 180/2 | 894611 | №57 | ||
| Двенадцатая звёздчатая форма икосододекаэдра | 300/3 | 1304011 | №58 | ||
| Тринадцатая звёздчатая форма икосододекаэдра | 120/2 | 11302011 | №59 | набор | |
| Четырнадцатая звёздчатая форма икосододекаэдра | 300/4 | 12458611 | №60 | ||
| Соединение большого звёздчатого додекаэдра и большого икосаэдра | 240/3 | 12598011 | №61 | ||
| Пятнадцатая звёздчатая форма икосододекаэдра | 420/5 | 1648411 | №62 | ||
| Шестнадцатая звёздчатая форма икосододекаэдра | 300/3 | 883811* | №63 | набор | |
| Семнадцатая звёздчатая форма икосододекаэдра | 180/2 | 8670011 | №64 | ||
| Восемнадцатая звёздчатая форма икосододекаэдра | 300/3 | 2049211* | №65 | ||
| Завершающая звёздчатая форма икосододекаэдра | 300/4 | 800211 | №66 | набор | |
| Невыпуклые однородные многогранники | |||||
| тетрагемигексаэдр | 16/2 | 800023 | №67 | есть, шаблон | |
| октагемиоктаэдр | 32/2 | 800024 | №68 | есть, шаблон | |
| малый кубокубоктаэдр | 62/4 | 800025 | №69 | набор | есть, шаблон |
| малый битригональный икосододекаэдр | 72/2 | 800026 | №70 | есть, шаблон | |
| малый икосоикосододекаэдр | 92/3 | 800027 | №71 | набор | |
| малый додекоикосододекаэдр | 152/4 | 800028 | №72 | есть, шаблон | |
| додекододекаэдр | 72/2 | 800029 | №73 | набор | есть, шаблон |
| малый ромбододекаэдр | 162/4 | 800030 | №74 | набор | есть, шаблон |
| усеченный большой додекаэдр | 72/2 | 800031 | №75 | ||
| ромбододекододекаэдр | 312/5 | 800032 | №76 | ||
| большой кубокубооктаэдр | 62/4 | 800033 | №77 | набор | |
| кубогемиоктаэдр | 30/2 | 800034 | №78 | есть, шаблон | |
| кубоусеченный кубооктаэдр | 62/4 | 800035 | №79 | ||
| битригональный додекаэдр | 192/3 | 800036 | №80 | ||
| большой битригональный додекоикосододекаэдр | 152/4 | 800037 | №81 | ||
| малый битригональный додекоикосододекаэдр | 212/4 | 800038 | №82 | ||
| икосододекододекаэдр | 432/6 | 800039 | №83 | ||
| икосододекоусеченный икосододекаэдр | 152/4 | 800040 | №84 | ||
| квазиромбокубоктаэдр | 488/14 | 800041 | №85 | ||
| малый ромбогексаэдр | 66/4 | 800043 | №86 | есть, шаблон | |
| большой битригональный икосододекаэдр | 300/4 | 800044 | №87 | набор | |
| большой икосоикосододекаэдр | 1232/15 | 800045 | №88 | ||
| малый икосогемидодекаэдр | 80/2 | 800046 | №89 | набор | есть, шаблон |
| малый додекоикосаэдр | 380/6 | 800047 | №90 | ||
| малый додекогемидодекаэдр | 72/2 | 800048 | №91 | есть, шаблон | |
| квазиусеченный гексаэдр | 54/3 | 800049 | №92 | ||
| квазиусеченный кубооктаэдр | 146/6 | 800050 | №93 | ||
| большой икосододекаэдр | 132/3 | 800051 | №94 | ||
| усеченный большой икосаэдр | 192/3 | 800052 | №95 | набор | |
| ромбоикосаэдр | 630/8 | 800053 | №96 | ||
| квазиусеченный звездчатый додекаэдр | 132/3 | 800054 | №97 | ||
| квазиусеченный додекаэдр | 402/6 | 800055 | №98 | ||
| большой додекоикосододекаэдр | 180/3 | 800056 | №99 | набор | |
| малый додекогемиикосаэдр | 132/2 | 800057 | №100 | ||
| большой додекоикосаэдр | 312/4 | 800058 | №101 | ||
| большой додекогемиикосаэдр | 312/5 | 800059 | №102 | ||
| большой ромбогексаэдр | 126/4 | 800060 | №103 | ||
| квазиусеченный большой звездчатый додекаэдр | 120/2 | 800061 | №104 | ||
| квазиромбоикосододекаэдр | 980/11 | 800062 | №105 | ||
| большой икосогемидодекаэдр | 180/3 | 800063 | №106 | ||
| большой додекогемидодекаэдр | 132/3 | 800064 | №107 | ||
| большой квазиусеченный икосододекаэдр | 1140/12 | 800065 | №108 | ||
| большой ромбододекаэдр | 612/8 | 800066 | №109 | ||
| малый курносый икосододекаэдр | 212/4 | 800067 | №110 | есть, шаблон | |
| курносый додекододекаэдр | 432/8 | 800068 | №111 | ||
| курносый икосододекододекаэдр | 452/9 | 800069 | №112 | ||
| большой вывернутый курносый икосододекаэдр | 300/5 | 800070 | №113 | ||
| вывернутый курносый додекододекаэдр | 372/7 | 800071 | №114 | ||
| большой курносый додекоикосододекаэдр | 600/10 | 800072 | №115 | ||
| большой курносый икосододекаэдр | 780/13 | 800073 | №116 | ||
| большой вывернутый обратнокурносый икосододекаэдр | 1800/30 | 800074 | №117 | ||
| малый вывернутый обратнокурносый икосоикосододекаэдр | 3060/28 | 800075 | №118 | ||
| большой биромбоикосододекаэдр | 1280/13 | 800076 | №119 | ||
| Разные призмы | |||||
| Пятиугольная призма | 7/2 | 800078 | набор | есть, шаблон | |
| Пятиугольная антипризма | 12/2 | 800086 | есть, шаблон | ||
| Пятиугольная звёздчатая призма | 12/2 | 800093 | есть, шаблон | ||
| Пятиугольная звёздчатая антипризма | 32/3 | 800100 | есть, шаблон |
Примечание: * Модели из книги Веннинджера №30, №55, №56, №63, №65 незначительно отличается от трехмерных моделей, представленные на сайте zvzd3d.ru. Это связано с тем, что на сайте звездчатые формы создаются автоматически специальным алгоритмом, заточенным на поиск наиболее красивых и разнообразных звёздчатых форм, в то время как Веннинджер выбирает звездчатые формы, наиболее простые с точки зрения изготовления модели из бумаги. Разность во внешнем виде моделей практически не заметна.
Лог запуска 3d-визуализатора
zvzd3d.ru © 2013-2021
Красивая геометрия
Украшать интерьер дома, создавая своими руками необычные, стильные вещи, — это увлекательное творчество. Смастерить самостоятельно из плотной бумаги различные многогранники — значит создать уникальные вещи, которые могут стать просто занятием на день или два, а могут превратиться в дизайнерские интерьерные украшения. К тому же с развитием техники, способной к пространственному моделированию всевозможных вещей, стало возможным создание стильных и современных 3D-моделей. Есть мастера, которые при помощи простроения разверток по законам геометрии делают из бумаги макеты животных и различных предметов. Но это достаточно сложное математическое и чертежное творчество. Начать работать в подобной технике поможет
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
Из бумаги
Из картона
Развертки куба
Треугольника
Прямоугольника
Цилиндра
Ромба
Призмы
Разные грани — разные формы
Многогранники — это особая сфера геометрии. Они бывают простые — к примеру кубики, которыми дети играют с раннего возраста, — а бывают очень и очень сложные. Простроение развертки многогранников для склеивания считается достаточно сложной областью конструирования и творчества: нужно не только знать основы черчения, геометрические особенности пространства, но и иметь пространственное воображение, позволяющее оценить правильность решения еще на стадии проектирования. Но и одной фантазией не обойтись. Чтобы сделать развертки не достаточно просто представить, как в конце концов должна выглядеть работа. Нужно уметь правильно ее просчитать, сконструировать, а также грамотно начертить.
Объемные поделки — животные из бумаги
Если говорить про поделки из бумаги для детей 4, 5, 6 лет, то одной из популярных тем для творчества является животный мир. Объемные зверушки из цветной бумаги, птицы, насекомые и рыбы словно оживают, приобретая не только яркую окраску, но и причудливую форму.
Мы подобрали специально для вас объемные поделки животных из бумаги, мастер-классы, шаблоны и пошаговые инструкции.
Мы рассмотрим в этой статье не просто примеры готовых работ, но также шаблоны объемных поделок, распечатать которые можно прямо с сайта.
Кроме самой бумаги и картона, нам также понадобятся ножницы, клей-карандаш (или ПВА), простой карандаш, некоторые дополнительные детали, например, втулки от туалетной бумаги и кукольные глазки. Кстати, игрушечные глазки можно сделать самостоятельно, вырезав маленький кружочек из белой бумаги и нарисовав на нем точку чёрным маркером.
Самый первый многогранник — кубик
Скорее всего, каждый человек, посещавший школу, еще в начальных классах сталкивался на уроках труда с работой, результатом которой должен был стать бумажный кубик. Чаще всего учительница раздавала заготовки — развертки многогранника куба на плотной бумаге со специальными кармашками, предназначенными для склеивания граней модели в единое целое. Такой работой ученики начальной школы могли гордиться, ведь при помощи бумаги, ножниц, клея и своих усилий получалась интересная поделка — трехмерный куб.
Занимательные грани
Удивительно, но многие знания об окружающем мире становятся интересны не на школьной скамье, а лишь тогда, когда можно найти в них нечто увлекательное, способное дать что-то новое, необычное в привычной жизни. Не многие взрослые помнят, что те же многогранники делятся на огромное количество видов и подвидов. Например, есть так называемые платоновы тела — выпуклые многогранники, состоящие только лишь из Таких тел всего пять: тетраэдр, октаэдр, гексаэдр (куб), икосаэдр, додекаэдр. Они представляют собой выпуклые фигуры без впадин. Звездчатые многогранники состоят из этих основных фигур в различных конфигурациях. Поэтому-то развертка многогранника простого позволяет нарисовать, вернее начерить, а затем и склеить из бумаги звездчатый многогранник.
Правильные и неправильные звездчатые многогранники
Складывая платоновые тела между собой в определенном порядке, вы можете построить немало звездчатых многоранников — красивых, сложных, многокомпонентных. Но они будут называться «неправильными звездчатыми многогранниками». Правильных звездчатых многогранников всего четыре: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Развертки многогранников для склеивания не будут простыми чертежами. Они, как и фигуры, будут состоять из нескольких компонентов. Так, например, малый звездчатый додекаэдр строится из 12 пятиугольных равнобочных пирамид, сложенных по типу правильного додекаэдра. То есть для начала придется начертить и склеить 12 одинаковых штук правильных пирамид, состоящих из 5 равных граней. И только затем из них можно сложить звездчатый многогранник. Развертка самого малого звездчатого додекаэра — сложное и практически невыполнимое задание. Чтобы ее простроить, нужно суметь на одной плоскости уместить соединенные друг с другом 13 разверток разных геометрических объемных тел.
Красота в простоте
Все объемные тела, построенные по законам геометрии, будут смотреться завораживающе, в том числе и звездчатый многогранник. Развертка каждого элемента любого подобного тела должна быть выполнена максимально точно. И даже самые простые объемные многогранники, начиная с платонового тетраэдра, — удивительная красота гармонии мироздания и труда человека, воплощенного в бумажной модели. Вот, допустим, самый многогранный из платоновых выпуклых многогранников — додекаэдр. В этой геометрической фигуре 12 абсолютно одинаковых граней, 30 ребер и 12 вершин.Чтобы сделать развертки правильных многогранников для склеивания, нужно приложить максимум аккуратности и внимательности. И чем крупнее фигура по размерам, тем точнее должны быть все измерения.
Как построить развертку самостоятельно?
Пожалуй, помимо склеивания многогранника — хоть звездчатого, хоть платоновского, — еще интереснее построить развертку будущей модели собственными силами, оценив свои способности к черчению, конструированию и пространственному вообжению. Простые платоновсткие тела состоят из простых многоугольников, которые в одной фигуре идентичны друг другу. Так, тетраэдр — это три равнобедренных треугольника. Прежде чем простроить развертку, нужно представить себе, как правильно сложить плоские многоугольники между собой, чтобы получить многогранник. Треугольники можно соединить между собой по ребрам, прочертив один рядом с другим. Для склеивания развертки многогранников схемы должны быть снабжены специальными кармашками или клапанами, которые позволят соединить все части в единое целое. Тетраэдр — простейшая фигура из четырех граней. Октаэдр можно представить как двойной тетраэдр, у него восемь гарней — равнобедренных треугольников. Гексаэдром называют знакомый всем с детства куб. Икосаэдр представляет собой соединение 20 равнобедренных треугольников в правильный выпуклый многогранник. Додекаэдр — это объемная фигура из 12 граней, каждая из которых представляет собой правильный пятиугольник.
Что такое тетраэдр
С помощью наглядной объемной фигуры детям проще научиться иметь представление о пространственном мышлении. В этом помогут объемные геометрические фигуры, сделанные своими руками из бумаги. Тетраэдр представляет собой многоугольную фигуру, которая считается простейшей. Он состоит из 4-х граней, каждая из них является равносторонним треугольником. Стороны треугольников соединяются между собой только одной гранью. В фигуре есть также четыре вершины и шесть ребер.
Людей с давних пор привлекали многогранники как удивительные символы симметрии. Они считали их божественными фигурами. Эти фигуры очень важны в развитии математического мышления детей дошкольного и школьного возраста. Они способствуют развитию геометрического представления и пространственного мышления.
На самом деле такая фигура встречается нам повсюду. Однако, сразу ее заметить сложно. Выполненная из стержней, она встречается как основа для пространственных конструкций:
- мостов;
- перекрытий;
- балок;
- ферм;
- пролетов зданий.
Для того чтобы получить такую фигуру, можно не прибегать к сложным математическим вычислениям. Полученная модель позволит иметь наглядное представление о свойствах геометрической фигуры в объемном изображении.
Тонкости работы
Построить разверту многогранника и склеить из нее бумажную модель — дело тонкое. Развертку, конечно, можно взять уже готовую. А можно, приложив услилия, построить ее самостоятельно. Но чтобы сделать полноценную объемную модель многогранника, нужно ее собрать. Многогранник лучше всего делать из плотной бумаги, которая хорошо держит форму и не коробится от клея. Все линии, которые необходимо согнуть, лучше всего предварительно продавить, используя, например, непишущую шариковую ручку или обратную сторону лезвия ножа. Этот нюанс поможет сложить модель аккуратнее, с соблюдением размеров и направлений ребер.
Если сделать разные многогранники из цветной бумаги, то такие модели можно использовать в качестве декоративных элементов, украшающих помещение — детскую комнату, кабинет, гостиную. Кстати, многогранники можно назвать уникальной находкой декораторов. Современные материалы позволяют на основе геометрических фигур создавать оригинальные предметы интерьера.
Варианты выполнения
Есть несколько способов выполнения фигуры, но лучше всего использовать самый простой и распространенный. В этом случае используется готовый шаблон, либо нужно нарисовать равносторонний треугольник. У фигуры на рисунке должны быть «лепестки», чтобы склеить их потом между собой.
При использовании собственного рисунка для склеивания есть свои преимущества. Для такой фигуры обычно берут бумагу разных цветов, что дает готовому изделию наглядный и интересный вид.
Во втором варианте применяют в склеивании не отдельные треугольники, а соединенные между собой. Такую заготовку называют разверткой тетраэдра. Лепестки находятся на всех открытых гранях треугольника либо на нескольких, для нормальной фиксации.
Более сложный способ — использование модульного варианта оригами. Для этого необходимо иметь достаточное количество бумаги, а главное — терпение и усидчивость. Поскольку такая работа кропотливая, она требует времени.
В любом из приведенных вариантов потребуется терпение и желание. В каждом из них есть свои преимущества. Выбор зависит от предназначения модели.
Необходимые материалы и инструменты
Для выполнения самого простого бумажного тетраэдра понадобятся следующие предметы:
- плотная цветная бумага (желательно картон);
- линейка;
- ножницы;
- транспортир;
- клей;
- инструкция (схема);
- тетраэдр из бумаги.
Очень важно перед началом выполнения работы ознакомиться с инструкцией. Это позволит получить одинаковые и идентичные стороны треугольника.
Развертка тетраэдра для склеивания
Ход работы будет зависеть от используемой бумаги. Если это картон, тогда необходимо для начала нарисовать развертку на бумаге. При использовании обычной бумаги развертка чертится прямо там.
Для начала нужно начертить прямую линию, которая является гранью фигуры. С двух сторон необходимо отметить углы по 60о. После этого полученные точки соединяются прямой линией до их пересечения. В итоге получается равносторонний треугольник.
После этого на каждой стороне полученного треугольника необходимо отложить такие же линии. Со всех концов откладываются 60о и снова соединяются прямой линией. В итоге при правильном выполнении получается схема их 4-х равносторонних треугольников.
Для получения хорошей и удобной для склеивания развертки необходимо сделать припуски по 1 см с 3-х сторон каждого треугольника. Если все выполнено правильно, получается чертеж, как на фото.
Теперь остается аккуратно вырезать развертку, согнуть все линии, а припуски загнуть внутрь. При необходимости можно обрезать уголки. Теперь их нужно промазать клеем, стыкуя линию сгиба между стороной и припуском к стороне свободного треугольника. Припуски прижимаются к внутренним сторонам граней.











 ,
, ,
, ,
, от Светланы
от Светланы